Statistical Analysis - 1

Independent Sample t-Test and A/B Test

Theory

Assumptions:

1. X and Y are independent
2. X and Y have same variance $\sigma^2$
3. X and Y from normal distribution, respectively

(*)Test Statistic Under Un-equal Variance

$$T=\dfrac{(\bar{X}-\bar{Y})-(\mu_X-\mu_Y)}{\sqrt{\dfrac{S^2_X}{N_X}+\dfrac{S^2_Y}{N_Y} } } \sim t\ (df)$$ $$df=\dfrac{\left(\dfrac{s^2_X}{N_Y}+\dfrac{s^2_Y}{N_Y}\right)^2}{\dfrac{(s^2_X/N_X)^2}{N_X-1}+\dfrac{(s^2_Y/N_Y)^2}{N_Y-1} }$$

Test Statistic Under Equal Variance

• Under Normal Distribution (Independent Sample T-test):

$$\hat \sigma_X = S_X,\hat \sigma_Y = S_Y$$ $$T = \frac{(\bar X - \bar Y) - (\mu_X - \mu_Y)}{\hat \sigma _{\bar X - \bar Y} } \sim \ t\ (df=N_X+N_Y-2)$$ $$\hat \sigma _{\bar X - \bar Y} = {s _{\bar X - \bar Y} } = s_p\sqrt{\frac{1}{N_X}+\frac{1}{N_Y} } \xrightarrow{N_X = N_Y} s_p \sqrt \frac{2}{N}$$ $$unbiased:\ s_p^2 = \frac{(N_X-1)\hat \sigma_X^2 + (N_Y-1)\hat \sigma_Y^2}{N_X+N_Y-2}\xrightarrow{N_X = N_Y} \frac{1}{2}(\sigma_X^2 + \sigma_Y^2)\xrightarrow{\sigma_X^2 = \sigma_Y^2} \sigma^2$$

• Under Binomial Distribution (A/B Test):
  • Option 1: Assume same proportion

$$\hat p = \frac{\hat p_X N_X + \hat p_Y N_Y}{N_X + N_Y} = \frac{1_X + 1_Y}{N_X + N_Y}$$ $$s_p = \sqrt{\hat p(1- \hat p)}$$ $$Z=\frac{\hat p_X-\hat p_Y}{\sqrt{\hat p(1-\hat p)(\frac{1}{N_X} + \frac{1}{N_Y})} } \sim N(0,1)$$

• Option 2: Assume different proportion

$$Z=\dfrac{\hat p_X-\hat p_Y}{\sqrt{\dfrac{\hat p_X(1-\hat p_X)}{N_X}+\dfrac{\hat p_Y(1-\hat p_Y)}{N_Y} } }$$

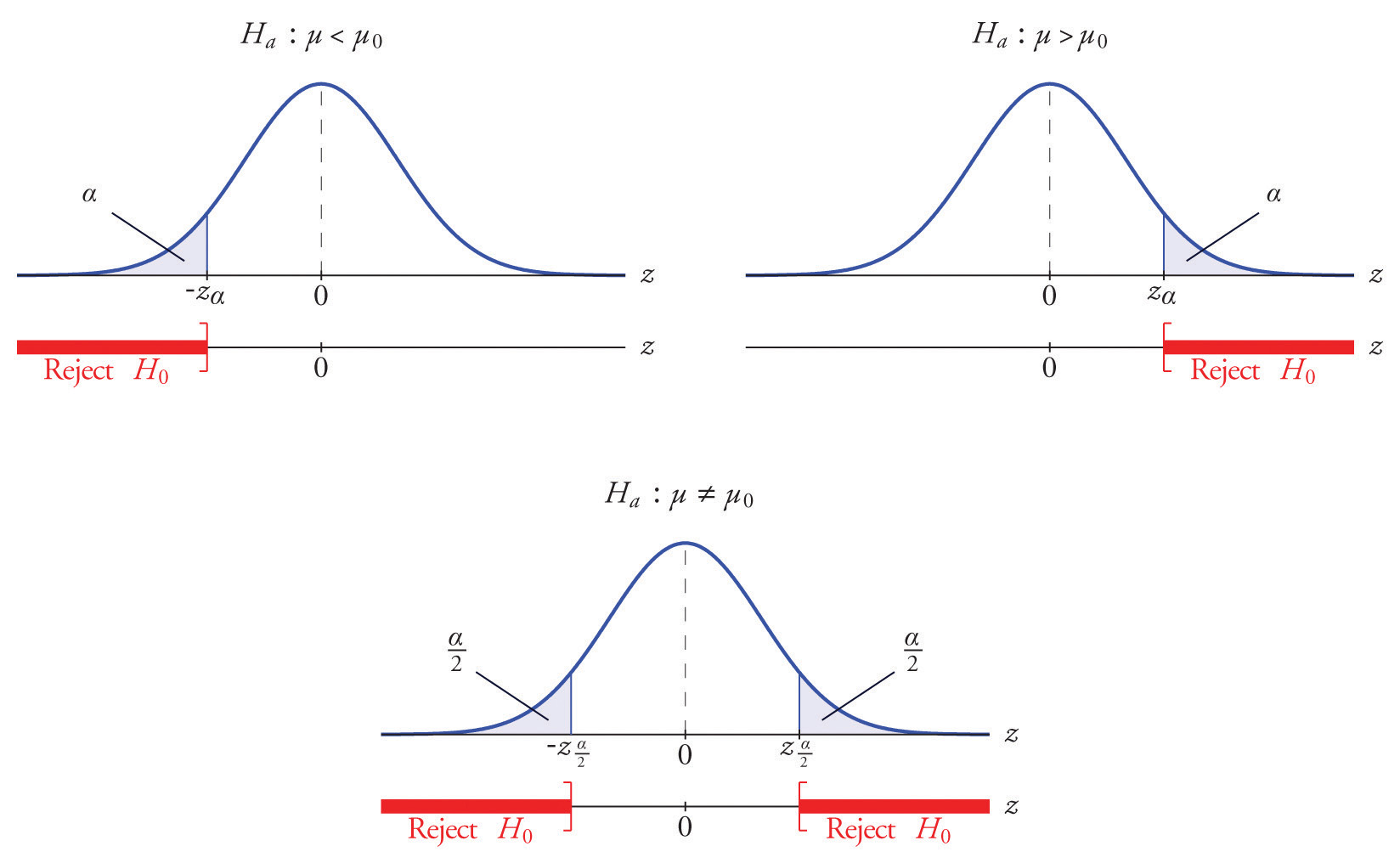
One-Tail vs. Two-Tail Test

• Two Tail: Compare $ \vert T \vert $ with $t _{m+n-2} (\alpha/2) $
• One-Tail: Compare $T$ with $t _{m+n-2}(\alpha)$

Violation of assumptions

• For $1^{st}$ assumption (Independence) : by experiment design

• For $2^{nd}$ assumption: Perform *Levene test *
  • Null hypothesis: samples have same variances
  • Reject null hypothesis when $p<\alpha=0.05$
  • When violated, the calculation of $df$ will change
  • Alternative: perform log transformation to stablize variation
• For 3rd assumption: Perform Shapiro-Wilks test
  • Reject null hypothesis when $p<\alpha=0.05$
  • When sample size is big, still valid (asymptotic normality)
  • Reason: Central Limit Theory for $\bar X$ and $\bar Y$

Relationship with Likelihood-Ratio Test

• Can be proved to be equivalent

Non-parametric methods

• Mann-Whitney Test: https://en.wikipedia.org/wiki/Mann%E2%80%93Whitney_U_test

• Wilcoxon Rank Sum Test

$${\displaystyle U _{1}=R _{1}-{n _{1}(n _{1}+1) \over 2}\,\!}$$

• Advantages
  • Small sample size
  • Robust to outliers
  • No need for normal assumptions
• Disadvantages:
  • Higher Type II error
  • Lower power
  • Not really needed for large sample

Calculate sample size / Power

Power:

• $P$(reject $H_0 \vert H_1$ is true)
• Commonly 80-95%
• Red shaded area

What impacts power

• Effect Size (+)
• Sample Size (+)
• Significant Level (e.g., 5%) (+)
• Population SD (-)
  • Conversion Rate vs. Actual number of visits

• ref: https://onlinecourses.science.psu.edu/stat414/node/304/

• Combined equation

$$ES = (t _{\alpha/2} + t _{\beta})s_p\sqrt{\frac{1}{N_1}+\frac{1}{N_2} }\xrightarrow{\sigma_1 = \sigma_2, N_1 = N_2} = (t _{\alpha/2} + t _{\beta})\sigma\sqrt{\frac{2}{N} }$$

• Effect Size

• Significance Level

• Calculate sample size

p_baseline = 0.50 # under H_0
effect_size = 0.05 # Desired effect size
sig = 0.99
sample_size = 1001
#https://onlinecourses.science.psu.edu/stat414/node/306/

• Look up table: $Z(\alpha) = 2.326$

• Calculate power of test
  • Standardize user-provided $ES$
  $$ES _{N(0,1)} = \frac{ES}{ \sigma _{p = \bar X} } = \frac{ES}{\sigma _{X} / \sqrt{N} } = \frac{ES}{\sqrt{\frac{p(1-p)}{N} } }$$
  • Calculate the arrow point on blue axis:
  $$- ES _{N(0,1)} + Z _{critical}$$
  • Calculate the area of blue
  $$\phi_z(- ES _{N(0,1)} + Z _{critical})$$
  • Calculate the area of power
  $$1-\phi_z(- ES _{N(0,1)} + Z _{critical})$$
• How to calculate Sample Size:
  • Formula for sample size estimation under $95\%$ significance and $80\%$ power.

$$N=\frac{16\sigma^2}{\Delta^2}$$

s_x = np.sqrt(p_baseline * (1 - p_baseline))
s_x

0.5

s_p =  s_x * np.sqrt( 1 / sample_size)
s_p

0.01580348853102535

effect_size_N_0_1 = effect_size / s_p
effect_size_N_0_1

3.163858403911275

phi_value = 2.326 - effect_size_N_0_1
phi_value

-0.8378584039112749

blue_shade = norm.cdf(phi_value)
blue_shade

0.2010551163605569

power = 1 - blue_shade
power

0.798944883639443

#Just use formula
N_size = 16 * p_baseline * (1 - p_baseline) / (effect_size * effect_size)
N_size

1599.9999999999998

Online Experiment

A/A Test

• Assign user to one of the two groups, but expose them to exactly same experience
• Calculate variability for power calculation
• Test the experimentation system (reject $H_0$ about 5% given significant level as 5%, with dummy treatments)

• Shut down treatment if significantly underperform

• Maybe something is wrong with how system assign treatment to users

Type of variates

• Call to action
• Visual elements
• Buttons
• Text
  • Ad: Promotion vs. Benefit vs. Information
  • Tweets: length/style/emoji/etc
• Image and Video
• Hashtags
• Backend (e.g., recommendation algorithm)

Select evaluation metric

• Short-term vs. Long-term
  • adding more ads –> short-term revenue
  • loss of page views/clicks –> long-term revenue loss / user abandonment
• Consistent with long-term company goal, and sensitive enough to be detected
  • KPI: hard to detect change in a short time
  • Evaluation metric: strong correlation with KPI as a proxy
• Example of metrics:
  • Netflix Subscription: Viewing hours
  • Coursera Course certification: Test completion / Course Engagement

• By selecting better evaluation metric

  • Search Engine: Sessions per user instead of queries per user
  • $\frac{Queries}{Month}=\frac{Queries}{Session}\times\frac{Session}{User}\times\frac{User}{Month}$

• By quantifying loss of traffic:

  • Putting Ad on Homepage: (decrease in click-through rate) X (visit frequency) X (cost of regenerating this traffic from other sources)

Limitations

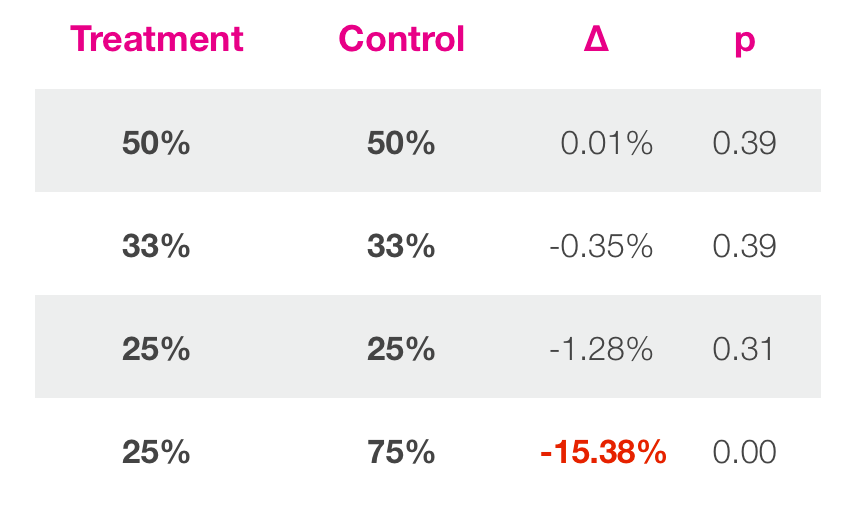
• Analyze across key segments
  • Browser type
  • Device type
  • New and return users
  • Men and women
  • Geo
  • Age
  • Subscribers

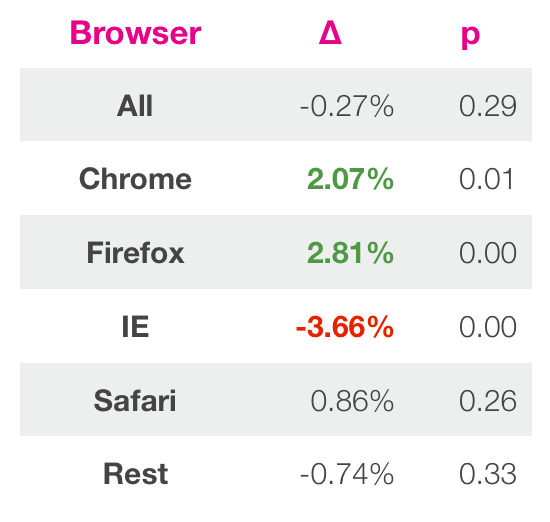
  Alert: Multiple comparison issue.

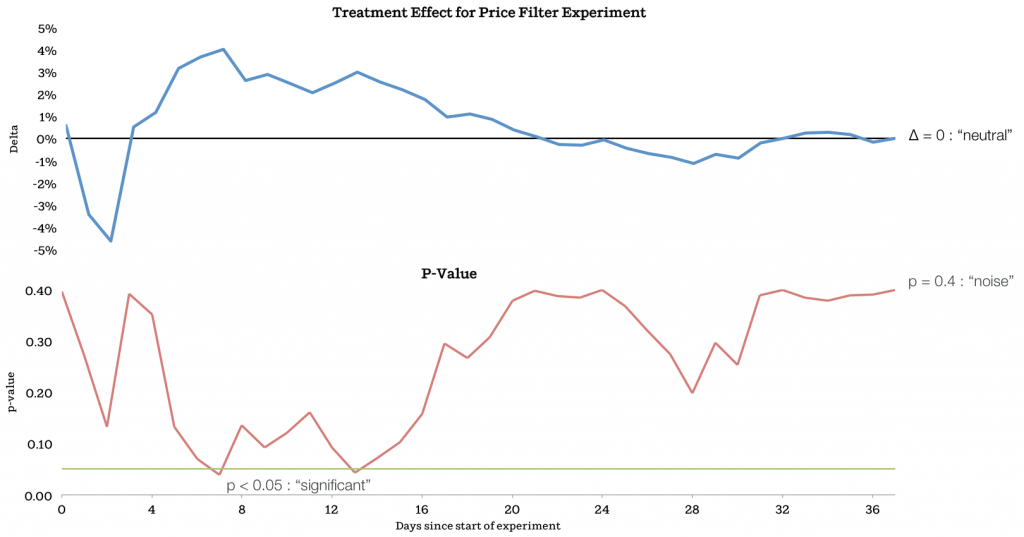
• Temporal factors (non-stationary time-series)
  • e.g, day of week effect
  • other periodical events
• Treatment ramp-up
  • Start from 0.1% treatment, gradually to 50%
  • A 50%/50% design is much faster than a 99%/1% design (25 times faster)

• Early stopping

• Preference to old or preference to newness
  • Novelty effect
  • Longer time
  • Only expose to new users
• Implementation cost
• Performance speed
  • Slow feature: bad experience

AB test vs. Bandit

Network effect

• Sample consistency: for example, GCP, two uses in one collaboration group faces two different features. Or adding a video chatting feature, which only works if both sides have access to it

• Sample independency (Spillover effect), for example, Facebook: many connected components, thus Group A and B are no longer independent.

• Possible solution: community (cluster) based AB test by partitioning nodes to groups, or for a dating app with no prior connections, maybe using demographic/geographical attributes
• Each cluster is assigned a treatment, thus unlikely for spillover from control to treatment
• Unit of analysis is reduced, higher variance as a result

Ref: http://web.media.mit.edu/~msaveski/projects/2016_network-ab-testing.html

Case Study

Problem Statement

• Given a feature difference in facebook app, evaluate if the change will improve user activity.
• Given a UI component change (e.g., button color) in a pageview, evaluate if there are more users clicking.
• Given a pop-up message, whether users will continue enroll in program or not
• Given a new firewall feature in GCP

http://rajivgrover1984.blogspot.com/2015/11/ab-testing-overview.html

For example: An online education company tested a change where if the student clicked “start free trial”, they were asked how much time they had available to devote to the course. If the student indicated 5 or more hours per week, they would be taken through the checkout process as usual. If they indicated fewer than 5 hours per week, a message would appear indicating that these courses usually require a greater time commitment for successful completion, and suggesting that the student might like to access the course materials for free.

Choose Subject (Unit of diversion)

Possible Choice:

• User id
• Cookie
• Event

Choose metric

Example of pop-up message and program enrollment

Guardrail Metrics that should NOT change:

• Number of cookies, unique # of cookies visiting the page
• Number of clicks on the button (since message shown after clicking)

Metrics that MAY change:

• User Aquisition: $p = \frac{Number\ of\ users\ actually\ enrolled}{Number\ of\ users\ clicking\ button}$

• User Retention: $p = \frac{Number\ of\ users\ remain\ enrolled\ for\ 14\ days}{Number\ of\ users\ clicking\ button}$

User Growth